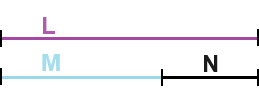
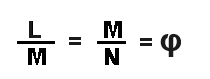or The Golden Ratio
1.618033988749894...
|
The mathematical constant known as "phi" is abbreviated by the lower-case Greek letter "φ". This constant is known by many names such as the golden ratio, the golden section, the golden mean, the divine proportion or the extreme and mean ratio. The concept of the phi ratio has existed for thousands of years, and has been utilized by artists, designers and a great many other professions. Basically it is the belief that the most pleasing artistic proportion (for horizontally-oriented art) is 1.62 (x axis) by 1 (y axis) or 1 by 1.62 for vertically-oriented art. Perhaps
the best way to describe the phi ratio is to state its two
properties: 1 ÷ φ = φ minus 1 2) The number phi squared equals phi plus 1 or stated mathematically: φ2 = φ + 1
Here
is another way to conceptualize the number "phi".
You
are no doubt familiar with the "Fibonacci Number Sequence"
in which a number sequence is built where each number is the sum
of the previous two numbers. 1 + 1 = 2 3 + 5 = 8 13 + 21 = 34
Geometrically speaking, the phi ratio appears in many geometric diagrams. 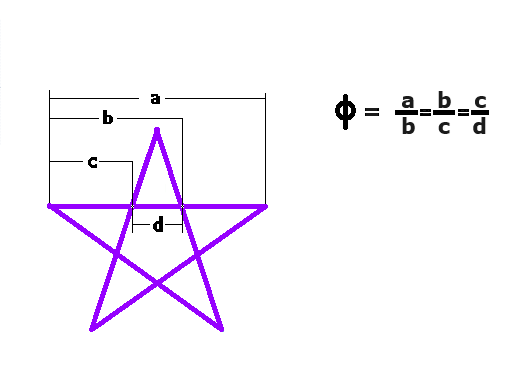 Looking at the pentagram diagram we can see that 4 of its line segments have been labeled.
We can see that: line segment a ÷ line segment b = φ line segment b ÷ line segment c = φ line segment c ÷ line segment d = φ By using this quadratic equation φ2 -φ -1 = 0 we can solve for phi using the quadratic formula where a = 1 b = -1 c = -1 : φ = [--1 +- Sqr Root (-1)2 - 4 * 1 * -1] / 2*1 φ = [(1 + Sqr Root (1 + 4))] / 2
*********************************************************** The other angle equals 222.463...° or 3.88271... radians. ************************************************************************ After presenting you with a great deal of information about the number phi, you should know that a great many people exaggerate the importance of it. As previously mentioned, phi does have some important mathematical properties but if you surf the Internet, you'll find all kinds of dubious "information". For example one of these allegedly important facts states that if you divide your height by the distance of your navel to the ground, it will equal 1.62. Even if it did equal 1.62 for every person in the world, what would this signify and why is your 'navel-to-ground' distance so vital? In medical school, do they teach doctors about measuring this crucial distance? ********************************************************************* |